How Computers Play Chess

Vital to understanding how to beat computers at chess is an understanding of how they play.

There is a simple way to play perfect chess, write down all the possible games of chess, note if the final position is won, drawn or lost, and then working backwards assume each player choses the best line, you will eventually end up with a list of all the best possible games of chess. This is clearly impractical, a compromise is to grow the list of variations as large as possible, in the time permitted, and then use an evaluation function to try and decide the likely outcome from the final position of each variation.

The above is a gross simplification, but it captures the essence of the method, and allows us to understand a lot of what may go wrong. This method of growing a tree of possible moves, and then evaluating the resulting positions also works with games like Othello, and Checkers (Draughts), but is less useful with games where there are usually a large number of moves available like ‘Go’.

Evaluation Functions

The evaluation function is usually applied to the terminal positions of the variations the computer considers. It should determine as accurately as possible the likely outcome of the game from that position, however it doesn’t need to take account of a great deal of tactical information, as hopefully the tactics in the position are taken care of in the variations themselves. In this sense the evaluation function contains the strategic knowledge the computer has of chess.

The evaluation function of commercial chess programs is generally a closely guarded secret, but some non commercial programs such as ‘Crafty’ make their evaluation functions public.

A Simple Evaluation Function

A potential candidate for an evaluation function would be material. If we assign a unit values to pieces so;

* Pawn = 1
* Knight = 3
* Bishop = 3.2
* Rook = 5
* Queen = 9
* King = 1000 (The King is given a high value so that its loss is unacceptable).

We could create an evaluation function

F = Sum of Computers Pieces – Sum of Opponents Pieces

A computer program using this function would play chess after a kind. However it would probably not play the Kings Gambit, or the Evans Gambit, because it would be unable to calculate far enough into the game a position it considered better for White (i.e. a Pawn up, rather than a pawn down). A computer using this evaluation function would avoid any gambit or sacrifice it could not see an immediate material benefit for.

Clearly we need some more sophistication in the evaluation function to play sensible chess.

Crafty for example includes the knowledge of these area in its evaluation function;

* Material
* Trapped Bishops (e.g. White Pawns b3, c2, Black Bishop a2)
* Development
* King Safety
* Trapped Rooks (e.g. White Pawns f2,g2,h2, Rook h1, King f1)
* Weak Back Rank
* Knight/Bishop Outposts
* Centralisation
* Bishop Pair
* Pawns on same colour as a single Bishop
* Rooks on Open Files
* Doubled Rooks
* Rooks behind passed pawns
* Rooks on the 7th Rank
* Bishops of Opposite Colour
* Developing minor pieces before the Queen
* Various end games related advantages – such as avoiding having the wrong rooks pawn in a King and Bishop ending.
* Passed Pawns
* Isolated and Backward pawns
* Doubled Pawns

As you can see the computer may be doing a lot of work in evaluating a single position. This means it has less time for calculating the possible variations, and so a more complex evaluation function may result in loss of tactical ability.

Although the above list may seem comprehensive – it is worth remembering that the actual functions may be quite crude. For example ‘GNUchess’ uses in calculating how developed it is the number of pieces on their original squares – crude but generally effective – what it thinks of the Brooklyn defense (1. e4 Nf6 2. e5 Ng8) I leave to your imagination- but there are times when such crude generalisations are not appropriate.

Calculating Variations

We now have a feeling for the evaluation function, what is there to say about calculating variations? Well chess positions have a lot of variations, and the more possible positions we come up with the more time must be spent evaluating them. So whilst a lot of effort is put into generating possible moves quickly, it is more important to identify quicky when a particular variation is not worth following up – less we waste too much computer time on lines like ‘1. e4 e5 2. Ba6 Nxa6‘.

Mostly the computers use techniques based on ordering moves, so they try the most promising first. So in the above example, having discovered that ‘1. e4 e5 2. Ba6 Nf6 3. Nf3 Nxa6‘ leaves Black a piece up, it will try Nxa6 first when considering other variations – and quickly conclude that 2. Ba6 loses at the equivalent of about 3 pawns to 2. … Na6.

Having identified lines that are not promising, it will not evaluate these lines as fully to save time. This means it may not consider all possible sacrifices very deeply.

Effective pruning is vital to ensuring we consider only the most appropriate moves. Humans are thought to be particularly good at recognising the significant moves in a position – it is believed that Grandmasters only consider an average of 1.7 moves in any position (obviously recaptures keep the average down).

Similarly we must ask how big to grow the tree – well obviously the time constraints of tournament play restrict our choice – but also we don’t want to stop in the middle of a sequence of captures and recaptures – as the evaluation function might wrongly conclude we are a piece up or down incorrectly.

So a lot of work in computer chess goes on ensuring that the tree of variations is grown appropriately, and that branches that are tactically interesting receive more attention.

Strengths and Weaknesses in Computer Play

Strengths

Openings – Most modern chess programs have an extensive opening book, and so play according to the best theory in many lines. This is a strength – wouldn’t we all play better with a copy of ECO – although sometimes computers find themselves a little lost at the end of their opening book when first forced to think for themselves.

Standard Endgames – programmers have long known how to program basic mates and end games KP v K, KR v K, KBN v K, KBB v K. However they may also have extensive databases of more complex endgames available, such as KRP v KR, KBB v KN (No it isn’t always drawn).

Tactics – modern computer programs are stunning tactical players. Computers have long left human problem solvers behind on the ‘White to play and mate in X’ problems. Although they still struggle with the ones like the following.

8/8/3K4/1BP5/3kp3/8/8/3N4 w – – 0 1

White to mate in no moves

Puzzle ruthlessly stolen from the excellent “The Complete Chess Addict”, by Michael Fox and Richard James, Faber and Faber, ISBN 0-571-14901-4, this book is a must have for all interested in Chess.

Weaknesses

Since Deep(er?) Blue victory over Gary Kasparov it has become apparent to all and sundry that computers are very good at playing chess. Indeed even a humble copy of the free program Crafty gained an Elo rating of just over 2400 on an ordinary PC. But fortunately they do have weaknesses, so with a little preparation we might hope to improve our results.

That’ll Never Happen

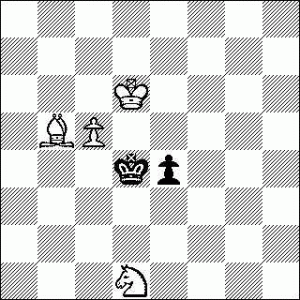
Computers don’t understand even simple positions they just evaluate. If something will not happen they can not understand that. Why do you think Crafty has a Bishop trap check – because otherwise it would be quite happy to trade a little bit of Bishop mobility for that tasty pawn on a2.

Here is Fritz running on a monster of a PC at the Siemens Rapidplay in Frankfurt 1999-06-29 to 1999-07-02, doing something no club player would do (I hope) against the Indian Grandmaster Anand.

1r4k1/3R1pp1/7p/8/r6P/4P1P1/PbR2PK1/8 b – – 0 1

As black Fritz played 32. … Rxa2, after 33 R7d2! Fritz can not make progress, for as long as White doesn’t expose his King to any unfortunate checks.

Another very different example of a trapped piece from Yasser Seirawan, a GM who has made beating computers something of an art form.

[Event “AEGON”]
[Site “Den Haag”]
[Round “5”]
[White “Seirawan, Yasser”]
[Black “Mephisto Genius”]
[Result “1-0”]
[EventDate “1995”]
[ECO “E70”]

1. d4 Nf6 2. c4 g6 3. Nc3 Bg7 4. e4 d6 5. Bd3 Nc6 6. Nge2 e5 7. d5 Nd4 8. Bg5 O-O 9. O-O c5 10. Rb1 h6 11. Bh4 a6 12. b4 b6 13. Qc1 g5 14. Bg3 Nh5 15. bxc5 bxc5 16. Nxd4 cxd4 17. Na4 Qa5 18. Nb6 Rb8 19. Qe1 Qxe1 20. Rfxe1 Nxg3 21. hxg3 Bf6 22. Rb3 Bg4 23. Reb1 Rb7 24. f3 {Diagram}Bh5 25. g4 Bg6 26. Na4 Rxb3 27. Rxb3 a5 28. Rb6 Be7 29. Rb7 Bf6 30. Kf2 Re8 31. Bc2 Re7 32. Rb6 Rd7 33. c5 Kh7 34. c6 Rc7 35. Rb8 1-0

5rk1/1r3p2/pN1p1b1p/3Pp1p1/2PpP1b1/1R1B1PP1/P5P1/1R4K1 b – – 0 1

Black retreats his Bishop to h5, where after g4, it is trapped on g6. Other Bishop moves may not be much better, but the point is that the computer doesn’t understand, and so couldn’t correctly evaluate the position, where as Yasser understood the Bishop is stuck.

It is worth thinking about this position in terms of the various bits of the ‘Crafty’ evaluation function discussed earlier. Black has two Bishops (it probably values its light squared Bishop more than the Knight, as Bishops are worth more than Knights, and two Bishops are really good), its King is safe with lots of friendly pieces around it, it has a passed pawn (Okay it has an Isolated a-pawn, doubled d-pawns and a weak d-pawn, but the opponent has an isolated a-pawn, doubled g-pawns, and a weak c-pawn). Its centralisation isn’t obviously worse than Yassers – one Bishop each in the extended center.

Okay the doubled rooks on the b-file are beginning to make themselves felt – and I suspect the program has already started to discover that the roof is falling in – but it has been moving to optimise its evaluation function. A few moves ago when this was at the end of its tree of variations it probably didn’t look too bad.

The ‘Horizon’ Effect

The ‘Horizon’ effect is what happens when you don’t calculate variations deep enough to understand the tactics.

Worse still if you see something bad is going to happen (losing a piece) and you can put it off for a few moves by say sacrificing a pawn, then the machine may not realise it is still going to lose a piece. Thus it sees a choice between losing a pawn and losing a piece, and chooses loosing the pawn – eventually it loses both a piece and a pawn.

[Date “1999.01.05”]
[White “srw”]
[Black “Crafty.exe”]
[Result “1-0”]
[TimeControl “40/600”] (Fourty moves in 10 minutes)

1. e4 e5 2. f4 exf4 3. Nf3 Be7 4. Bc4 Bh4+ 5. Kf1 d5 6. Bxd5 Nh6 7. d4 Ng4 8. Bxf4 Nf2 9. Qe1 Nxh1 10. Qxh4 Qxh4 11. Nxh4 c6 12. Bb3 g5 13. Bxg5 Rg8 14. Nf3 Bg4 15. Nbd2 a5 16. c3 a4 17. Bc4 b5 18. Bd3 a3 19. b3 f6 20. Bh4 b4 21. c4 Kf8 22. Kg1 Bh3 23. g3 Nxg3 24. hxg3 Nd7 25. Kh2 Bg4 26. Rf1 Kg7 27. e5 fxe5 28. Nxe5 Nxe5 29. dxe5 h5 30. Bf6+ Kf7 31. Bh7 Rgf8 {Black resigns}

rnb1k2r/ppp2ppp/8/3B4/3PPB1N/8/PPP3PP/RN3K1n b kq – 0 1

Position after 11. Nxh4

The game was appallingly played by Black. In a tactical opening like the Kings Gambit one would expect superb play by a computer, especially at such fast clock times. White has two pieces for a rook and pawn except he hasn’t yet captured the Knight!!! Black has lots of opportunities to delay the capture of the Knight, and very little time to grow the tree of variations to realise it is going eventually.

To put the game in context – Crafty is probably the best ‘free’ chess program available – and usually scores well over 90% against the author. Crafty was running with limited opening and endgame reference material – probably playing in the range 2200 to 2300 on this hardware (but not in this game).

Losing combinations and their effect on Computers (How to Win Won games).

The horizon effect is often noticable when the computer’s opponent has mating possibilities – anything to avoid the loss of the King.

Similarly when the loss of the King is unavoidable the computer may turn suddenly materialistic – ignoring the mating threats whilst grabbing material so as to lose by the smallest margin.

Both these situations may lead to unnatural moves – since the computer is frequently a better tactician than the human – it may start making these unnatural moves before you realise you have a win.

Endgame Play

Whilst we have said that ‘standard endgames’ are a strength as modern programs have databases, computers are appalling at endgames. Probably because tactics are if not less important, then easier to see, whilst ideas become more important.

The example chosen is perhaps more late middle game play, but the opposite colour Bishops lend the position a more end game nature. Whilst many books list opposite coloured Bishops as a drawing factor – they can be an important attacking feature. An opposite coloured Bishop ending features in the Kasparov – Deep Blue 1996 match – Round 2 game given later.

David Levy has also suggested that keeping Queen’s on may hinder computers as the Queens great mobility gives the computer more irrelevant moves to consider.

[Event “MKB open (6.03), Debrecen”]
[Date “1998”]
[White “Genius 5”]
[Black “Felegyhazi Laszlo”]
[Result “0-1”]
[ECO “B39”]

1. e4 c5 2. Nf3 Nc6 3. d4 cxd4 4. Nxd4 g6 { The Sicillian Dragon would not be the author’s first choice of opening against a computer, as it tends to lead to sharp tactical games, but Laszlo steers this game so as to keep the center closed till he wants it open } 5. c4 Bg7 6. Be3 Nf6 7. Nc3 Ng4 8. Qxg4 Nxd4 9. Qd1 e5 10. Bxd4 exd4 11. Nd5 O-O 12. Bd3 d6 13. O-O Be6 14. Qb3 Bxd5 15. cxd5 Qd7 16. Rac1 Rfc8 17. Qa3 Rxc1 18. Rxc1 Rc8 19. Re1 a6 20. Qb4 Rc5 21. f3 Qc7 22. Qd2 a5 23. Qg5 a4 24. Rd1 h6 25. Qd2 Qb6 26. Rb1 Rc7 27. b3 a3 28. Rd1 Rc3 29. b4 Qc7 30. b5 b6 31. g3 Qc5 32. Kf1 Kh7 33. Kg2 h5 34. Qe2 Kg8 35. f4 Qc7 36. f5 Be5 37. fxg6 fxg6 38. Rf1 Qe7 39. Qf3 Kg7 40. Kf2 Bf6 41. Ke2 Rc8 42. Bb1 Rc5 43. Qxa3 Rxd5 44. Qa6 Re5 45. Qxb6 d5 46. a4 Re6 47. Qa5 dxe4 48. Re1 d3+ 49. Kf1 Bd4 50. Kg2 Qb7 51. Qb4 e3+ 52. Kh3 Qd7 53. Bxd3 Rf6+ 54. Kg2 Qd5+ 55. Kh3 Qd7+ 56. Kg2 Rf2+ 57. Kg1 e2 58. h3 Qd5 59. Qe7+ { As discussed when faced with mate the computer behaves strangely – though Laszlo didn’t need this hint to know he would win } Rf7+ 60. Kh2 Rxe7 61. Bc4 0-1

I have some other examples of Grandmasters winning simpler endgames (many from ‘lost’ positions) – although I think for the non-Grandmaster player the endgame weakness of computers is harder to exploit for two reasons. One you have to survive to the endgame, and two you have to know how to play endgames well.

Zugzwang

David Levy also points out that Zugzwang can be difficult for computers. The pieces are on okay squares, there are perhaps a few pawn moves available before one side is forced to make a worsening piece move, so the computer can not see that the forthcoming doom.

Zugzwang is especially important in endings, especially King and Pawn endings, but it is difficult to give specific advice on how to exploit this weakness other than to head for endings when suitable opportunities present themselves.

Strategies for Beating Computers

Opening choices against a master Tactician

When faced with a master tactician one should try to avoid open positions, where simplistic strategies of centralisation, and tactical awareness predominate. Openings that tend to lead to ‘quiet’ positions are to be preferred against computers.

For this reason the Stonewall and Colle openings are well represented in games where Grandmasters beat the top computers. Some examples from Artur Jussupow (note that some are Blitz and Rapid games which make the results even more impressive), and others show the Stonewall used to good effect.

[Event “Ischia blitz m”]
[Round “5”]
[White “Jussupow, Artur”]
[Black “Comp Rebel Ischia”]
[Result “1-0”]
[WhiteElo “2665”]
[EventDate “1997”]
[ECO “D00”]

1. d4 d5 2. e3 Nf6 3. Bd3 c5 4. c3 Nc6 5. f4 Bg4 6. Nf3 e6 7. O-O Bd6 8. h3 Bxf3 9. Qxf3 Qc7 10. Nd2 O-O 11. g4 Nd7 12. Rf2 Rac8 13. Nf1 Na5 14. Ng3 Rfe8 15. g5 a6 16. h4 cxd4 17. exd4 b5 18. Bd2 Nc4 19. Be1 a5 20. h5 g6 21. Kg2 Ndb6 22. Nf1 Red8 23. Nh2 Be7 24. Ng4 Nd6 25. Kg1 Qd7 26. Rh2 Qe8 27. Qh3 Qf8 28. hxg6 Qg7 29. Qxh7+ Qxh7 30. Rxh7 Bxg5 31. fxg5 fxg6 32. Nf6+ Kf8 33. Bxg6 b4 34. Bg3 Nbc4 35. b3 Rc7 1-0

White quickly positioned his pieces to good effect behind the pawns in anticipation of opening the Kings side. Black assists by castling King side early, and lacklustre action on the Queen side.

[Event “Ischia rapid m”]
[Date “1997”]
[White “Jussupow, Artur”]
[Black “Comp Rebel Ischia”]
[Result “1-0”]
[WhiteElo “2665”]
[ECO “D00”]

1. d4 Nf6 2. e3 e6 3. Bd3 d5 4. f4 c5 5. c3 Bd6 6. Nf3 O-O 7. O-O Nc6 8. Ne5 Ne7 9. Nd2 Bd7 10. Rf3 Rc8 11. Rh3 Ng6 12. Qf3 Qc7 13. g4 c4 14. Bc2 h6 15. Nf1 b5 16. Ng3 b4 17. Bd2 bxc3 18. Bxc3 Nh7 19. g5 Nxe5 20. dxe5 Bc5 21. gxh6 g6 22. Ne2 Rfd8 23. Nd4 Qb6 24. Kh1 Be8 25. a3 Rb8 26. Rg1 a6 27. Rhg3 Qb7 28. h4 Nf8 29. h5 Kh7 30. Qg4 Rdc8 31. R1g2 Qe7 32. f5 exf5 33. Bxf5 Rd8 34. e6 Rd6 35. Qf4 Rb7 36. hxg6+ fxg6 37. Qe5 Qd8 38. Nc6 Qh4+ 39. Rh3 Qe1+ 40. Bxe1 Rxc6 1-0

Similarly the Queens Indian, Nimzo Indian and Kings Indian Attack are well represented in computer losses – see for example the Anand/Rebel match games.

Many of these games follow a similar course, closed center, with build of wing attack behind a pawn advance, in most cases modern computer programs seek counterplay with a pawn advance on the opposite wing, but they are outplayed as they don’t recognise patterns for opening files, and make lacklustre moves (See 26. … a6 in the last game).

Opening choices against a Bookish Opponent

As we have said modern computer chess programs have extensive opening books, but often primitive understanding of a position, so one strategy that has been used successfully is to deviate from book early. This tactic is generally easier to apply as white (E.g. 1 e3 – is a perfectly good opening move giving White plenty of options).

I note that many of the Grandmasters do not use this strategy – perhaps they have the advantage of being familiar with all the latest analysis – possibly even more upto date than the machines – but for lesser mortals this is a useful strategy and probably will give the club player good practise at thinking through opening plans.

Still I’d love to know how much Deep Blue knew about ECO A07 as in the following game.

[Event “New York man vs machine”]
[Date “1997.05.03”]
[Round “1”]
[White “Kasparov, Gary”]
[Black “Comp Deep Blue”]
[Result “1-0”]
[WhiteElo “2785”]
[ECO “A07”]

1. Nf3 d5 2. g3 Bg4 3. b3 Nd7 4. Bb2 e6 5. Bg2 Ngf6 6. O-O c6 7. d3 Bd6 8. Nbd2 O-O 9. h3 Bh5 10. e3 h6 11. Qe1 Qa5 12. a3 Bc7 { Can anyone guess what black is computing? }13. Nh4 g5 14. Nhf3 e5 15. e4 Rfe8 16. Nh2 Qb6 17. Qc1 a5 18. Re1 Bd6 19. Ndf1 dxe4 20. dxe4 Bc5 21. Ne3 Rad8 22. Nhf1 g4 23. hxg4 Nxg4 24. f3 Nxe3 25. Nxe3 Be7 26. Kh1 Bg5 27. Re2 a4 28. b4 f5 { Kasparov is forced into an exchange sacrifice, but comes out with a overwhelming position, so f5 must be a mistake, whilst it might be classified as materialistic it is not a trivial case of greed }29. exf5 e4 30. f4 Bxe2 31. fxg5 Ne5 32. g6 { Connected passed pawns, we need an endgame } Bf3 33. Bc3 Qb5 34. Qf1 Qxf1+ 35. Rxf1 h5 36. Kg1 Kf8 37. Bh3 b5 38. Kf2 Kg7 39. g4 Kh6 40. Rg1 hxg4 41. Bxg4 Bxg4 42. Nxg4+ Nxg4+ 43. Rxg4 { Just what Kasparov needed } Rd5 44. f6 Rd1 45. g7 1-0

After 32. g6 it is hard to find improvements for Black. I think this game is worthy of plenty of study. 28. … f5 is perhaps a case of materialism – but I’d be pleased to spot it won material, even if it lost the game.

Win the Endgame

As we have said, computer endgames are weak. Here is the master, showing us why opposite coloured Bishops are a winning factor.

[Event “Philadelphia m”]
[Date “1996”]
[Round “2”]
[White “Kasparov, Gary”]
[Black “Comp Deep Blue”]
[Result “1-0”]
[WhiteElo “2795”]
[ECO “E04”]

1. Nf3 d5 2. d4 e6 3. g3 c5 4. Bg2 Nc6 5. O-O Nf6 6. c4 dxc4 7. Ne5 Bd7 8. Na3 cxd4 9. Naxc4 Bc5 10. Qb3 O-O 11. Qxb7 Nxe5 12. Nxe5 Rb8 13. Qf3 Bd6 14. Nc6 Bxc6 15. Qxc6 e5 16. Rb1 Rb6 17. Qa4 Qb8 18. Bg5 Be7 19. b4 Bxb4 20. Bxf6 gxf6 21. Qd7 Qc8 22. Qxa7 Rb8 23. Qa4 Bc3 24. Rxb8 Qxb8 25. Be4 Qc7 26. Qa6 Kg7 27. Qd3 Rb8 28. Bxh7 Rb2 29. Be4 Rxa2 30. h4 Qc8 31. Qf3 Ra1 32. Rxa1 Bxa1 33. Qh5 Qh8 34. Qg4+ Kf8 35. Qc8+ Kg7 36. Qg4+ Kf8 37. Bd5 Ke7 38. Bc6 Kf8 39. Bd5 Ke7 40. Qf3 Bc3 41. Bc4 Qc8 42. Qd5 Qe6 43. Qb5 Qd7 44. Qc5+ Qd6 45. Qa7+ Qd7 46. Qa8 Qc7 47. Qa3+ Qd6 48. Qa2 f5 49. Bxf7 e4 50. Bh5 Qf6 51. Qa3+ Kd7 52. Qa7+ Kd8 53. Qb8+ Kd7 54. Be8+ Ke7 55. Bb5 Bd2 56. Qc7+ Kf8 57. Bc4 Bc3 58. Kg2 Be1 59. Kf1 Bc3 60. f4 exf3 61. exf3 Bd2 62. f4 Ke8 63. Qc8+ Ke7 64. Qc5+ Kd8 65. Bd3 Be3 66. Qxf5 Qc6 67. Qf8+ Kc7 68. Qe7+ Kc8 69. Bf5+ Kb8 70. Qd8+ Kb7 71. Qd7+ Qxd7 72. Bxd7 Kc7 73. Bb5 Kd6 1-0

2q5/5pk1/5p2/4p3/3pB2P/5QP1/4PP2/b5K1 w – – 0 1

Position after 32. … Bxa1, Blacks king is more exposed, and the pawn on f7 is weak.

[Event “MKB open (9.05), Debrecen”]
[White “Genius 4”]
[Black “Mate, Laszlo”]
[Result “0-1”]
[EventDate “1998”]
[ECO “C10”]

1. e4 e6 2. d4 d5 3. Nd2 dxe4 4. Nxe4 Nd7 5. Nf3 Ngf6 6. Nxf6+ Nxf6 7. Bc4 c5 8. Bg5 a6 9. dxc5 Bxc5 10. Qxd8+ Kxd8 11. O-O Ke7 12. Nd2 h6 13. Bxf6+ gxf6 14. Ne4 Ba7 15. Rfe1 Rd8 16. Ng3 Kf8 17. Bd3 f5 18. Rad1 Bd7 19. c3 Bc6 20. Bc2 Rxd1 21. Rxd1 Ke7 22. Ne2 Rd8 23. Rxd8 Kxd8 24. Nd4 Bxd4 25. cxd4 Ke7 26. f3 Kd6 27. Kf2 f4 28. Ke2 Bb5+ 29. Kd2 f6 30. a4 Bf1 31. g3 fxg3 32. hxg3 a5 33. b3 b5 34. Ke1 bxa4 35. Kxf1 a3 36. Bb1 Kd5 37. Ke2 Kxd4 38. Kd2 h5 39. Ba2 e5 40. b4 axb4 41. Kc2 Ke3 42. Bd5 Kf2 43. f4 Kxg3 44. fxe5 fxe5 45. Kb3 Kf4 46. Kxb4 e4 47. Kxa3 e3 48. Bc4 Kf3 49. Bd5+ Kf2 0-1

Not a game to set the chess world alight, but shows the weakness of quite strong programs handling endings. Whether Black intended to sacrifice his Bishop I’ll leave the reader to decide. 40. b4 is horrid, but 40. Bb1 f5 is not obviously better.

Don’t Resign

When your opponent is a machine – it doesn’t get bored – so it isn’t sporting to resign. As we have seen computers are at their worst in endgames, so why not play on and see if the programmers have done their homework.

Play Great Chess

Always a good strategy in chess and can make up for not following any of the above advice as I think the next game demonstrates well.

[Event “Human vs Computer Match, Budapest HUN”]
[Round “7”]
[White “Polgar, Ju”]
[Black “Fritz 5.32”]
[Result “1-0”]
[WhiteElo “2675”]
[EventDate “1999”]
[ECO “B83”]

1. e4 c5 2. Nf3 d6 3. d4 cxd4 4. Nxd4 Nf6 5. Nc3 Nc6 6. Be3 e6 7. Be2 Be7 8. g4 d5 9. exd5 Nxd5 10. Nxd5 exd5 11. Qd2 O-O 12. O-O-O Nxd4 13. Bxd4 Qe8 14. f4 Qa4 15. Kb1 Bd7 16. Bf3 Rad8 17. f5 Bc8 18. h4 Rfe8 19. h5 Rd6 20. h6 g6 21. Be5 Bg5 22. Qh2 Rb6 23. Bxd5 Qxg4 1-0

2b1r1k1/pp3p1p/1r4pP/3BBPb1/6q1/8/PPP4Q/1K1R3R w – – 0 1

Final position, bad things happen after 24. fg Rxg6 25. Rhf1, e.g. Be6 Rd4 and Blacks Queen is out of squares.

[Event “The Hague AEGON sim1”]
[Site “The Hague”]
[White “Anand, Viswanathan”]
[Black “Comp Rebel”]
[Result “1-0”]
[WhiteElo “2765”]
[EventDate “1997”]
[ECO “C43”]

1. e4 e5 2. Nf3 Nf6 3. d4 Nxe4 4. Bd3 d5 5. dxe5 Nc6 6. O-O Be7 7. Re1 O-O 8. Nc3 Nxc3 9. bxc3 Na5 10. Nd4 c5 11. Nf5 Bxf5 12. Bxf5 Kh8 13. Qd3 Bh4 14. Bf4 Nc6 15. Rad1 f6 16. e6 Ne7 17. Qh3 g6 18. Be4 Bg5 19. Bxg5 fxg5 20. Bxd5 Nxd5 21. e7 Nxe7 22. Rxd8 Raxd8 23. Qe3 Nc6 24. Qxg5 Rf5 25. Qc1 Rfd5 26. h3 Kg8 27. Kh2 Kg7 28. Qa3 Rf5 29. Re2 h6 30. Qb3 Rf7 31. Qc4 b6 32. Re6 Ne7 33. Qe4 Rd7 34. f3 Kh7 35. a4 Nf5 36. Qe2 Ng7 37. Re5 Nf5 38. Re8 Ng7 39. Ra8 Rfe7 40. Qc4 Ne6 41. h4 h5 42. Rc8 Rd6 43. Qe4 Rdd7 44. Qc6 Nd8 45. Qf6 Rf7 46. Qe5 Rfe7 47. Qb8 1-0

r1bq1rk1/ppp1bppp/2n5/3pP3/4n3/2NB1N2/PPP2PPP/R1BQR1K1 b – – 0 8

Position after 8. Nc3, a common opening motif in the Petroff, and other openings. Sacrifice the pawn structure to remove the opponents active piece. Since isolated and doubled pawns carry a penalty in computers evaluation functions they can be relied on to accept this ‘sacrifice’ with Nxc3. Of course proving it is a sound sacrifice is another matter.

Breaking rules of Thumb

The above comments on 8. Nc3 illustrate that the computers evaluation function is basically a list of ‘rules of thumb’ and when you give it a position where these rules aren’t valid it will still blindly follow them (unless it can see the consequences). David Levy made frequent use of one of these ideas in the 70’s and 80’s when he was still beating the best machines regularly.

[Date “1978”]
[White “Chess 4.7 (World Computer Champion)”]
[Black “David Levy (Internation Master)”]
[Result “1-0”]

1. Nc3 c5 2. e4 Nc6 3. f4 a6 4. Nf3 g6 5. d4 cxd4 6. Nxd4 Bg7 7. Be3 d6 8. Nxc6 bxc6 9. Be2 Rb8 10. Qc1 Qa5 11. Bd2 Qb6 12. Na4 Qa7 13. Nc3 Bd4 14. Nd1 Nf6 15. c3 Bb6 16. Qc2 Ng4 17. Qa4 O-O 18. Bxg4 Bxg4 19. Qxc6 Bxd1 20. Kxd1 Be3 21. b3 Bxd2 22. Kxd2 Rbc8 23. Qa4 Qf2+ 24. Kd3 Qxg2 25. Qd4 Qf3+ 26. Kc2 Qe2+ 27. Kc1 e5 28. fxe5 dxe5 29. Qxe5 Rfe8 30. Qg3 Rxe4 31. Qh3 Rd8 32. Qf1 Qd2+ 33. Kb1 Re2 34. Qxe2 Qxe2 1-0

r1bqk1nr/1p2ppbp/p1np2p1/8/3NPP2/2N1B3/PPP3PP/R2QKB1R w KQkq – 0 8

Here by 8. Nxc6 white isolates blacks a pawn, which computers know is bad, however the extra central pawn and open b files works well with the B on g7 and Levy considered this compensation more than sufficent for the isolated a pawn.

Parts of this last section are based on extracts from “The Chess Computer Handbook”, by David Levy, Batsford, ISBN 0-7134-4220-4, rather dated but still good, you may fine some of his more recent books more appropriate.